Lately, I have been doing some hardware security research, specifically focusing on side channel stuff, this inspired me to write these challenges for the 0xL4ugh CTF.

Tempus

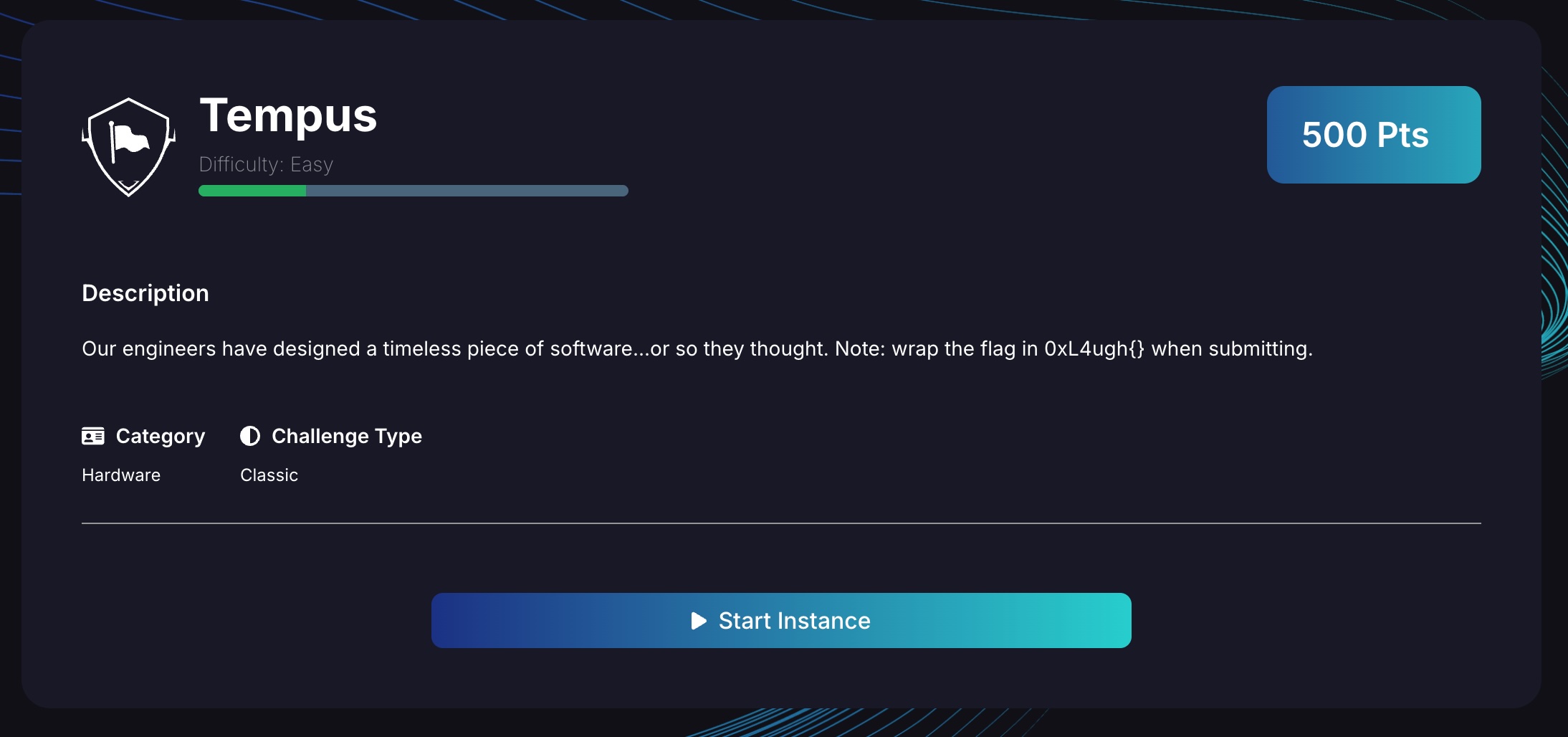
After spinning up the instance and connecting, we test the challenge logic.

The flag seems to be 9 digits long by elimination, so we know the length of the password. The next step was to check the timing of the responses for different digits. I used the time command to measure this, and it turns out that the digit ‘5’ takes significantly longer to process than the rest, hinting at a possible timing attack.

Non-constant time operations can pose a significant security risk, especially in cryptographic systems. This was demonstrated as early as 1996 by Kocher in his famous paper.

To find the letters of the correct password, we can use the following one-liner:

1

for i in {0..9}; do cat <(echo "$i") - | time nc localhost 11111 ; done

We don’t use echo directly but instead use it along with stdin as parameters for cat. This keeps the connection alive after the echo, and time will give us the correct timing once the netcat connection closes.

Using this one-liner we can start bruteforcing the flag digit by digit:

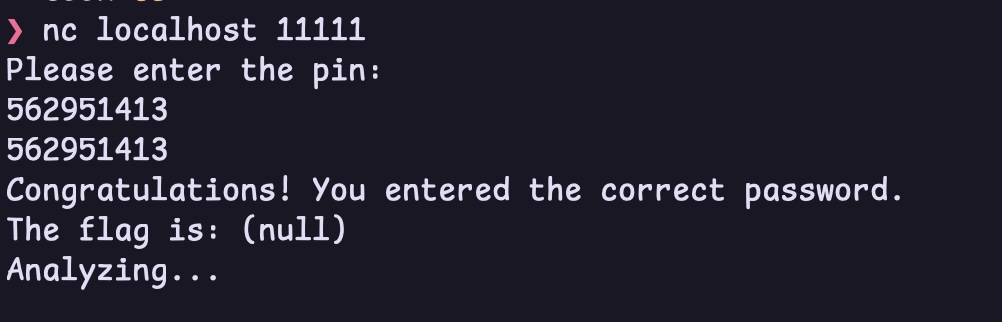
and the correct pin is 562951413.

Here’s the python solver as well:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

import time
from pwn import *
import string
import numpy as np
from tqdm import tqdm


def try_letter(letter):
    # io = process("./chal")
    # host = "f3c7d0159c523472a737fce4144226a6.chal.ctf.ae"
    # io = remote(host, 443, ssl=True, sni=host)
    io = remote('localhost', 11111)
    io.recvuntil("Please enter the pin:\r\n")
    start = time.perf_counter()
    io.sendline(letter)
    io.recvuntil("Analyzing...")
    diff = time.perf_counter() - start
    io.close()
    return diff

def get_timing(attempt, samples=5):
    times = [try_letter(attempt) for _ in range(samples)]
    return np.mean(times)

timings = {}
flag = ""
charset = string.digits

for i in range(9):
    timings.clear()

    for ch in tqdm(charset, position=0):
        timings[ch] = get_timing(flag + ch, samples=1)

    max_val = max(timings, key=timings.get)
    flag += max_val

    print(bytes(flag, encoding="utf-8"))

io = remote('localhost', 11111)
io.clean(1)
io.sendline(flag)
print(io.clean(1).decode())

Squinty

We are given some power traces in .npy format, which we can load in Python using np.load('traces.npy'). I used Plotly to generate the following plot:

We can see a repeating pattern of some data followed by 5 peaks. The 5 peaks are always constant and never change, but the data before them seems to vary. Let’s call the data followed by the five peaks a ‘segment.’ Going through our traces, we notice there are a total of 28 segments. Now, let’s focus on the first segment of our trace, which is shown below:

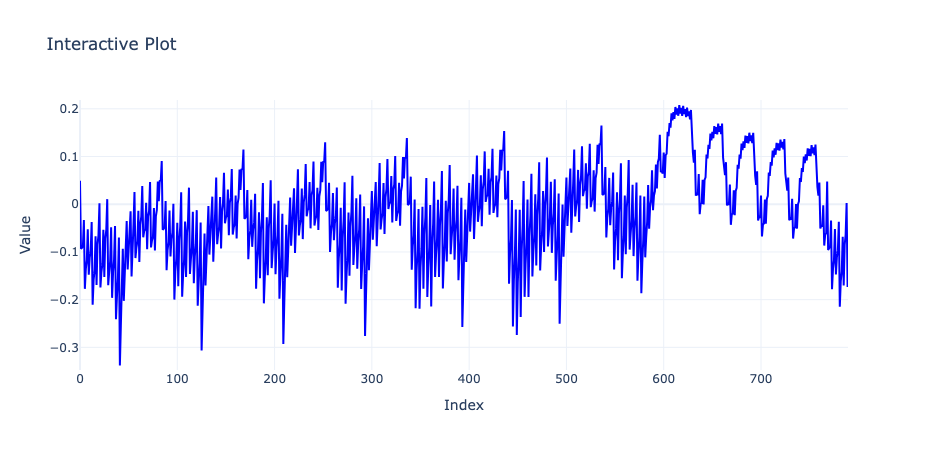
By examining closely, we can identify two distinct patterns repeated throughout the segment. We also know this is related to the square-and-multiply algorithm. I will take a moment to explain the square-and-multiply algorithm, as it is crucial for understanding this challenge.

Square and multiply is a modular exponentiation algorithm, and its most basic implementation is as follows:

1
2
3
4
5

while exponent > 0:
     if exponent % 2 == 1:  # If the current bit is 1
         result = (result * base) % modulus # Multiply
     base = (base * base) % modulus  # Square
     exponent = exponent // 2       # Move to the next bit

When implemented in its most basic form, this algorithm poses a security risk, especially in the context of hardware security. The major flaw is that the operation (and power consumption) is data-dependent, meaning the operation we perform depends on the values of the exponent bits.

The square and multiply operations in hardware are very architecture-dependent, and there is no single way to implement them. However, most of the time, these two operations will have unique power footprints and even timings. By inspecting power traces visually, we can easily identify which operation is which and, consequently, leak the exponent bits, as they depend on the operation. The image below illustrates this concept well:

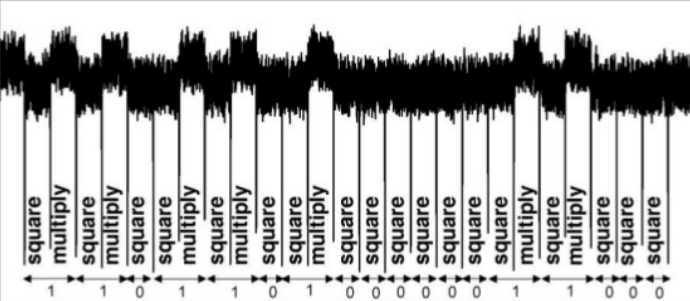
This means that a square pattern alone represents a 0 bit in the exponent, and a square pattern followed by a multiply pattern represents a 1. Note that this depends on the implementation; in this challenge, the multiply operation occurs before the squaring. With this information, we start looking for patterns in the segments of our provided trace.

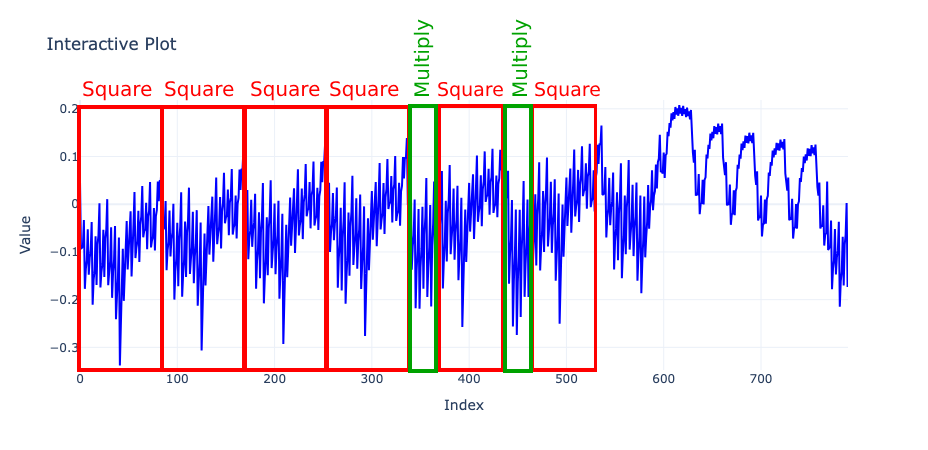
According to the challenge description, the flag starts with 0xL4ugh{, which means the first segment must correspond to the letter ‘0’, with an ASCII representation of 0x30 or 110000 in binary.

A plausible hypothesis is as follows:

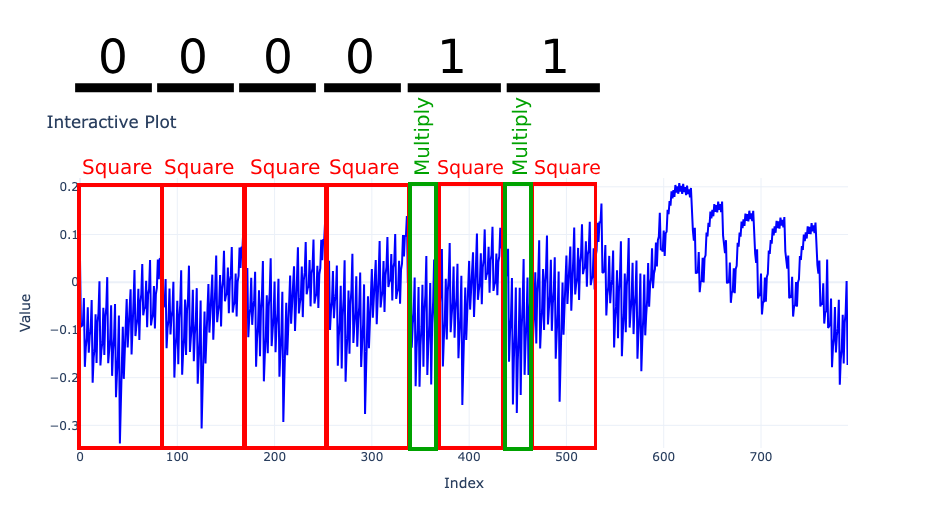
We reverse these bits since data is processed from LSB to MSB, which explains the reversed ASCII value. Here’s how we decode the second segment:

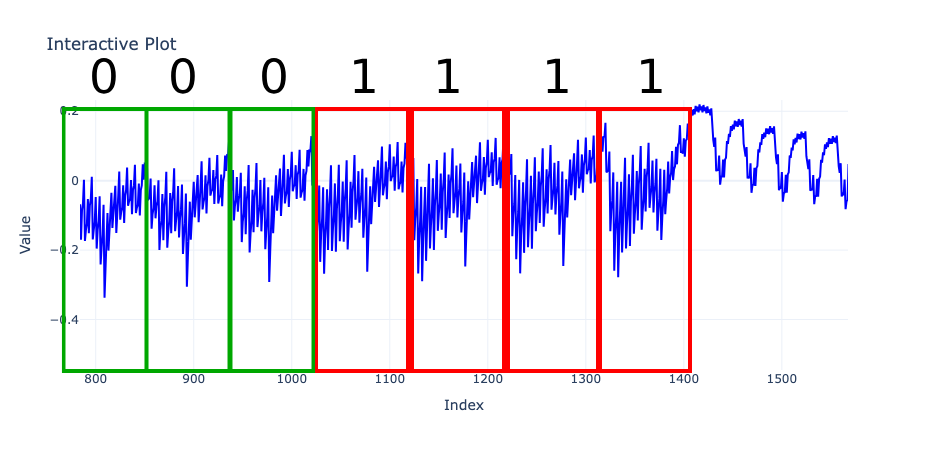
This decodes to ‘x’ after reversing the bits. By repeating this operation 26 more times, we end up with the flag: 0xL4ugh{Squinting4SPA_Sucks}.

This attack is known as Simple Power Analysis (SPA). It is a type of power analysis where data can be visually recovered in one shot without performing differential analysis or using multiple traces.

One of the players, yun., was able to automate solving this challenge using signal processing, which was quite interesting. You can find links to other write-ups at the end of this blog.

Power-SCAndal

This challenge is inspired by a similar one created by the ChipWhisperer team. If you’re interested, I highly recommend checking out this link and doing the rest of the exercises to improve your skills in SCA/Fault Injection.

Connecting to the challenge’s instance using netcat (or snicat) will exhibit the following behavior:

This outputs power traces for any input we provide. It returns an error when we input more than 8 characters and only accepts lowercase letters and digits. It’s important to note that the flag does not start with 0xL4ugh{ in this challenge. Therefore, I will start by plotting power traces and inspecting them visually.

Using the following code to parse the output and convert it to a NumPy array, I plotted the traces starting with the letter ‘a’:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

from pwn import *
import numpy as np

context.encoding = 'latin-1'
def get_trace(letter):
    io = remote("localhost", 22222)
    io.recvuntil("DEBUG> ")
    io.sendline(letter)
    io.recvuntil("\n")
    resp = io.recvuntil("]")
    io.close()
    array = np.fromstring(resp.decode().strip("[]"), sep=" ")
    return array

trace = get_trace("a")
plot(trace)

We get very similar traces when plotting ‘a’, ‘b’, ‘c’, and so on. Therefore, I decided to plot all the letters from ‘a’ to ‘z’ and the digits from ‘0’ to ‘9’, overlaying them in a single plot. Below is the result as an interactive plot:

By inspecting this plot, we can see a very clear outlier at the beginning of the trace, as shown in the picture below:

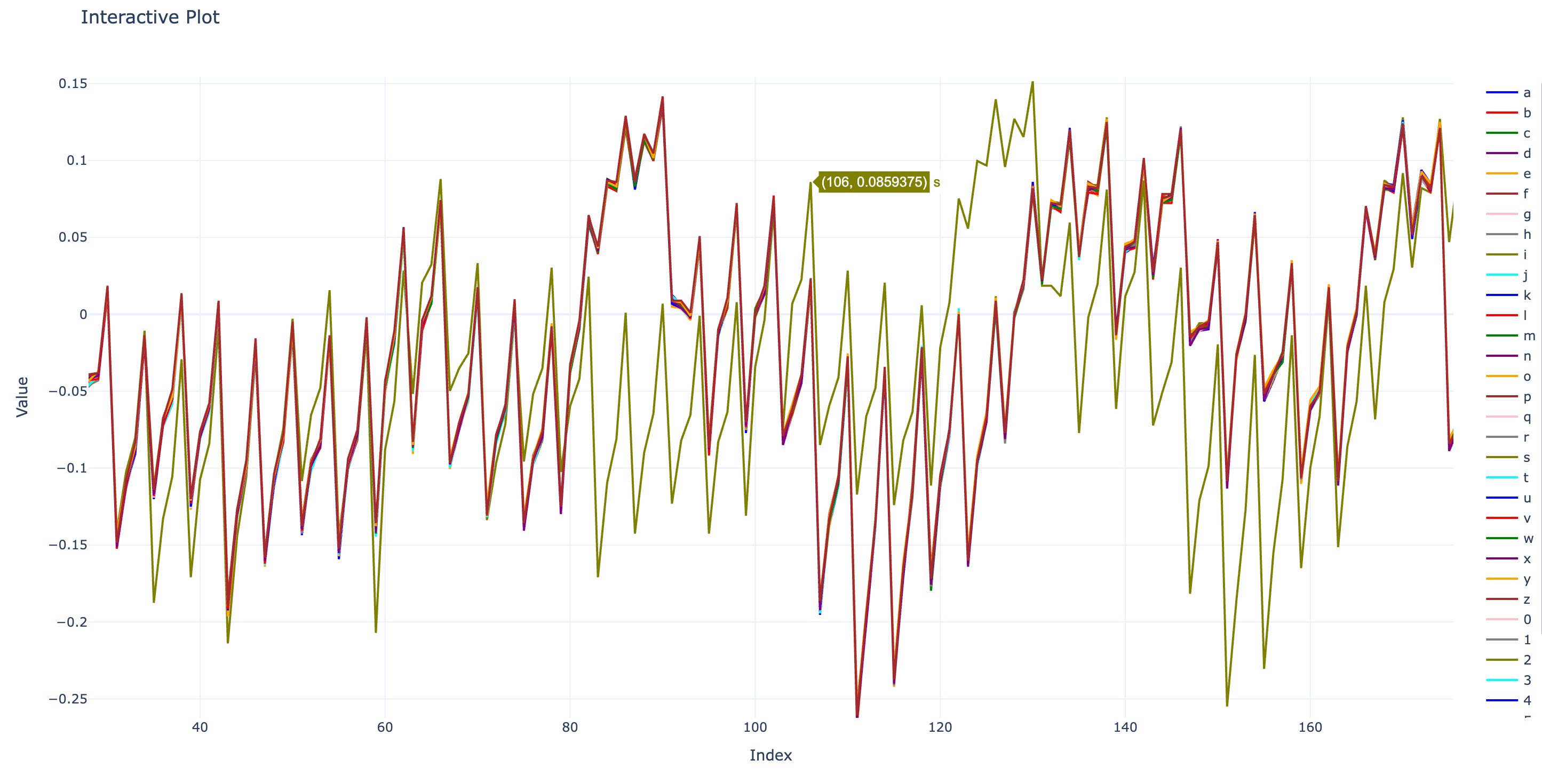
The outlier corresponds to the letter ’s’, suggesting that ’s’ is part of our flag. We can repeat this process by appending ’s’ to the charset loop to find that the second correct character is ‘h’. However, we can automate this process with a script.

We’ll use a statistical metric called Sum of Absolute Differences (SAD) as our distinguisher, which is popular in side-channel analysis. It’s a measure of similarity between two traces. By picking a random trace as a reference, we can run our solver multiple times to identify the consistent result and determine our flag.

Here’s the script to do this:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

from pwn import *
import numpy as np
import random
from tqdm import trange

context.encoding = 'latin-1'
def get_trace(letter):
    # host = "4b7339cb7c4f0e9673826d549734dae1.chal.ctf.ae"
    # io = remote(host, 443, ssl=True, sni=host)
    io = remote("localhost", 22222)
    io.recvuntil("DEBUG> ")
    io.sendline(letter)
    io.recvuntil("\n")
    resp = io.recvuntil("]")
    io.close()
    array = np.fromstring(resp.decode().strip("[]"), sep=" ")
    return array


passwd = ""
charset = "abcdefghijklmnopqrstuvwxyz0123456789"

for _ in trange(8):
    max_sad = 0
    correct_ch = ""
    ref = get_trace(passwd + random.choice(charset))
    for ch in charset:
        try:
            sad = np.sum(abs(ref - get_trace(passwd + ch)))
        except:
            print("Password is: ", passwd + ch)
            quit()
        if sad > max_sad:
            max_sad = sad
            correct_ch = ch
    passwd += correct_ch
    print(passwd)

Here are some links to other writeups If you are interested in other ways/methodologies to solve these challenges.

• https://github.com/r3-ck0/writeups/tree/master/0xl4ugh/hw/
• https://yun.ng/c/ctf/2024-0xl4ugh-ctf/hardware